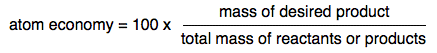|
Chemguide: Core Chemistry 14 - 16 Limiting reagent and atom economy calculations You won't find the terms limiting reagent and atom economy on all syllabuses, so check to see if you need to know about either of these. Limiting reagent calculations I am assuming in this section that you are happy with calculations from equations involving masses, solutions and volumes of gases. The example I am going to take involves all of these. If that is a problem, explore the rest of the calculations menu before you go on. (Link to the menu at the bottom of the page.) Consider the familiar reaction between calcium carbonate and dilute hydrochloric acid.
If you add a small amount of acid to a large amount of calcium carbonate, the reaction will soon stop because the acid is all used up. The acid is the limiting reagent - the amount of carbon dioxide is limited by the amount of acid present. On the other hand, if you had a tiny amount of calcium carbonate and added lots of acid, the reaction would stop when the calcium carbonate was all used up. In this case, the calcium carbonate is the limiting reagent. There is nothing difficult about this. The limiting reagent is the one which controls the amount of reaction you can get - in other words, the reagent which isn't in excess. This becomes important if you are trying to calculate the theoretical yield from a reaction involving a lot of ingredients. For example, one of my practical chemistry books gives a a recipe for preparing 1-bromobutane which starts from the following: 10 g sodium bromide 7.5 cm3 butan-1-ol 10 cm3 water 10 cm3 concentrated sulfuric acid You couldn't possibly work out the possible yield unless you knew which was the limiting reagent, and that would be a bothersome sum because you are given some things as volumes rather than masses, and so you would have to convert volumes into masses using density values. So we are going to take a simple example instead! Suppose you added 150 cm3 of 1.0 mol dm-3 hydrochloric acid to 5.0 g of calcium carbonate. What volume of carbon dioxide would you collect at room temperature and pressure? (RAMs; C = 12; O = 16; Ca = 40. Molar volume = 24 dm3 mol-1 at rtp.)
When you do most mole calculations you start with what you know most about and work out the number of moles. But in this case, you know everything necessary about both reagents. What you don't know is which is in excess. So work out the number of moles of both of them.
Now compare the numbers of moles. The calcium carbonate needs 0.10 mol HCl; you have 0.15 mol. So the acid is in excess. Now we can calculate the volume of carbon dioxide produced based ot the calcium carbonate present.
| |
|
Note: I have deliberately included all the other variants of calculations from equations in this sum (apart from titration calculations) so that you can check that you are happy with them. I can't include titration calculations because they involve knowing that you have exactly the right proportions with nothing in excess and no limiting reagent. | |
|
Atom economy Suppose you take a reaction like the one that produces the iron in a Blast Furnace - the reaction between iron(III) oxide and carbon monoxide.
You have no real interest in anything apart from the iron produced. Carbon dioxide is an unwelcome by-product, but you are bound to get it using this reaction. Atom economy can be defined as:
It doesn't matter whether you calculate this from the total mass of the reactants or the products, because they are going to be the same if you work from a balanced equation. It also doesn't matter what mass units you use, because you are simply finding a ratio. The easiest thing to do is just to calculate the total mass from the relative formula masses. In this case: RAMs: C = 12; O = 16; Fe = 56
I'm not going to go any further with this. If you want a lot more examples and a discussion around them, then you can go to this page on Doc Brown's website which includes the example I have used here.
© Jim Clark 2021 |
|