|
Chemguide: Core Chemistry 14 - 16 Measuring enthalpy change practically This page introduces the term "enthalpy change" and looks at how it can be measured using simple lab experiments. You need to check your syllabus and past papers to find out how much of this you need to know. Enthalpy change I am assuming that you already know about endothermic and exothermic reactions. If not, explore the energy menu before you go on.
It is no more difficult than that! It is given the symbol ΔH - read as "delta H". The enthalpy change is always based on the reactants. If a reaction gives out heat, the reactants must have lost that amount of energy, and so ΔH is given a negative value, such as -100 kJ mol-1 (read as "kilojoules per mole"). If a reaction absorbs heat, then the reactants must have gained heat and so ΔH is given a positive value, such as +50 kJ mol-1. So . . .
It is essential that you get those the right way round. Measuring enthalpy changes Enthalpy changes are found by measuring the temperature change produced by the reaction. If the reaction includes a liquid, you can measure the temperature change of the liquid. If you are finding the enthalpy change of combustion, you can use the heat produced to warm up some water, and measure the temperature increase in that. A bit of physics Specific heat capacity In the olden days, a calorie was defined as the amount of heat necessary to raise the temperature of 1 g of water by 1 °C. That is called the specific heat capacity of water. | |
|
Note: The common everyday use of the word calorie actually refers to kilocalories. | |
|
Nowadays, the joule has replaced the calorie as the unit of heat, and 1 calorie is equivalent to 4.18 joules. So the specific heat capacity of water is now 4.18 J g-1 °C-1 You read that as "4.18 joules per gram per degree Celcius". In every case, the specific heat capacity of any substance is the number of joules needed to raise the temperature of 1 g of it by 1 °C. So you can work out the amount of heat produced by a reaction using
Also written as:
The symbol Δ (delta) means "change in". If you had an endothermic change, then you would have to rephrase that as
Measuring the enthalpy change of combustion of ethanol The video shows a simple method for doing this in a school lab. The interesting bit about this video is the discussion of the errors involved. The presenter says at the end ". . . the enthalpy of combustion you will see is rather lower than data book values". That will turn out to be an understatement! Let's take the experimental results from this video and calculate the enthalpy change of combustion of ethanol.
The first thing to do is to calculate the amount of heat given off using the formula above. We make the assumption that the only thing being heated is the water in the calorimeter. That of course, is nonsense! We are also heating the copper calorimeter, the gauze, the metal support, the stirrer, the thermometer, and the air - and this is the major source of error. And, of course, you have to add on other errors like incomplete combustion and insufficiently accurate thermometers.
I am only quoting this to 2 significant figures. Even that is a greater accuracy than the experiment deserves! Enthalpy changes are always quoted in kilojoules, so we first need to divide this value by 1000.
That was given out when 0.42 g of ethanol were burned. How much would be evolved when 1 mole is burned? (RAMs: H = 1; C = 12; O = 16)
The enthalpy change of combustion of ethanol is therefore -440 kJ mol-1. (The negative sign showing that the reaction is exothermic.) And the data book value? -1371 kJ mol-1. This is a spectacularly bad result - but it doesn't matter in this context. We have seen how the experiment might be done, and looked at the major errors involved which suggest that this isn't a realistic way of getting an accurate result. And we have shown how you can process the results. Accurate results need access to equipment which you won't normally find in a school lab. Measuring the enthalpy change of the reaction between copper(II) sulfate solution and zinc
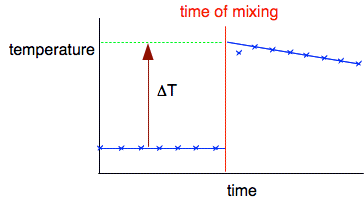
You can get much better results in reactions like this which can be done in a polystyrene cup. The polystyrene is a good insulator and has a very low mass, so hardly any heat will be used in warming that up. The next video is quite long. You will have to ignore the unconventional spelling! I suggest you pause the video at 5:26 and ignore the rest of it which deals with the calculation. That is better done written down - as below. I need to discuss the purpose of the graph, so keep that on the screen before you read on. The reason for the graph The temperature rise is quite large (48°C), and at that temperature heat will be being lost - for example, through the uninsulated lid. You can see the effect of that heat loss by the fact that the graph starts to fall when the reaction is over. You can compensate for the heat loss by extrapolating the cooling part of the graph back to the time of mixing to give a better estimate of what the maximum temperature would be in the absence of any heat loss. You plot enough points before mixing in order to be sure that the liquid is at constant room temperature. Then you get a quick rise in temperature as the reaction happens before it starts to cool again.
Once you have established that the cooling is happening at a steady rate, you extrapolate the cooling curve back to the point of mixing to give a reasonable estimate of the temperature rise you would have got if there was no cooling. It is then an easy job to measure the overall temperature rise, ΔT. Results
Calculation
| |
|
Note: The negative sign shows that the reaction was exothermic. If the last stage of the calculation (dividing 5.016 by 0.025) worries you, replace the 0.025 by a simpler number like 2. If 2 moles produced 5.016 kJ, 1 mole would obviously produce half that. You divided by 2. There is no reason for doing anything different whatever number of moles of copper(II) sulfate you have. | |
|
Comments If you watched the video to the end, you were told that the accepted value for this enthalpy change was -219 kJ mol-1. So this result is in the right area, but is still about 10% adrift. There are several problems with this calculation.
Don't worry about this unless you have to account for a value found from your own experiment. If you are asked something like this in an exam, the numbers will probably be made up anyway to give a reasonable answer.
© Jim Clark 2021 |
|