Chemguide: Core Chemistry 14 - 16

The effect of temperature on the rates of chemical reactions

This page explains why changing the temperature changes reaction rates, and introduces the concept of activation energy.

The overall effect

As a rough and ready guide, increasing the temperature by 10°C doubles the rate of a reaction.

You mustn't take this too literally. It doesn't apply to all reactions. Even where it is approximately true, it may be that the rate doubles every 9°C or 11°C or whatever. The number of degrees needed to double the rate will also change gradually as the temperature increases.

Explaining this in terms of the collision rate

Heating something up makes the particles move faster. If they move faster, they will collide more often - and so the possibility of a reaction happening increases.

The trouble with this explanation is that it only makes up a very tiny proportion of the observed change in reaction rate as you increase the temperature.

For a typical reaction around room temperature, if you increase the temperature by 10°C, the collision rate only increases by a bit less than 2%. But the reaction rate will approximately double - an increase of about 100%.

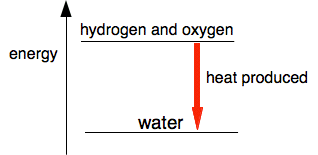
Activation energy

On that page, you will have found this simple energy diagram for the reaction between hydrogen and oxygen.

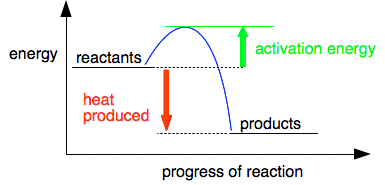
This is a very exothermic reaction, giving out a lot of heat when the gases combine to make water. The system becomes more energetically stable after the hydrogen and oxygen combine together.

So why don't hydrogen and oxygen react immediately on mixing if they become more stable by reacting?

For any reaction to happen, bonds need to be broken, and new bonds formed. Breaking bonds costs energy; energy is released when new bonds form.

In the reaction between hydrogen and oxygen, you have to put quite a lot of energy in to break the bonds in the hydrogen and oxygen molecules.

In a hydrogen / oxygen mixture at ordinary temperatures, collisions between the molecules don't generate enough energy to achieve this.

The minimum amount of energy needed for a collision to produce a reaction is called the activation energy.

We can modify the last diagram to show this. This is called a reaction profile. The diagram below serves for any exothermic reaction.

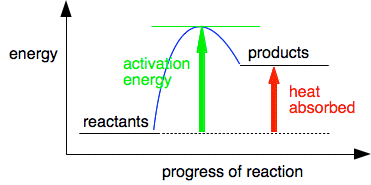
You can draw a similar diagram for an endothermic reaction.

This time, of course, the activation energy is much greater.

Temperature and energy

The temperature of a substance is related to the average kinetic energy of its particles. If the average kinetic energy goes up, you will see that as an increase in temperature.

But this is an average kinetic energy. Within that, individual particles may have quite a low energy, or a moderate energy or a very high energy - and that will be changing all the time as particles collide with each other.

However, the average will still stay the same at a particular temperature.

What we are really interested in from the point of view of reaction rates are the particles which have high enough energies at the time so that when they collide, they reach activation energy.

The particles with moderate or low energies will just bump off each other again without any reaction happening.

KE = ½mv²

Explaining the effect of temperature on rates in terms of activation energy

For a reaction to happen, collisions must generate an energy equal to or greater than activation energy. So we are only interested in those particles which have very high kinetic energies at that time.

Increasing the temperature doesn't have the same proportional effect on all the particles. Instead, it produces a big increase in the number of the most active particles.

So the main influence of temperature on reaction rates is to produce a large increase in the number of particles whose collisions will have energies equal to or greater than activation energy.

Illustrating the effect of temperature using an experiment

A commonly used experiment to show the effect of temperature on rate is the reaction between dilute hydrochloric acid and sodium thiosulfate solution which you will already have seen on the page about the effect of concentration on reaction rates.

Na₂S₂O₃(aq) + 2HCl(aq)  2NaCl(aq) + SO₂(g) + S(s) + H₂O(l)

This time all the concentrations and volumes of solutions are kept constant, but the temperature of the reaction is varied.

The video shows this happening by mixing increasing amounts of cold sodium thiosulfate solution with a warm solution of the same concentration.

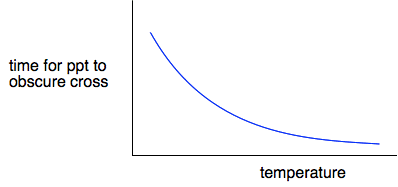
If you plot time taken for the cross to disappear against temperature, you get a graph which looks like this.

Clearly, the higher the temperature, the shorter time it takes for the cross to disappear, and so the faster the reaction.

Does this bear out the approximation that a 10°C temperature rise roughly doubles the rate of reaction? You can find that out by looking at the graph on the video.

At 20°C, it takes about 250 seconds; at 30°C, it takes about 125 seconds. It has halved the time for the cross to disappear, and so doubled the rate.

At 40°C, the time taken is between 60 and 70 seconds - approximately halved again and so another doubling of the rate.

In this case, there is no point in drawing a graph of 1/t (as a measure of rate) against temperature. A doubling of rate for every 10°C rise wouldn't produce a straight line - it would just give another (but different) curve.