NON-IDEAL MIXTURES OF LIQUIDS

This page looks at the phase diagrams for non-ideal mixtures of liquids, and introduces the idea of an azeotropic mixture (also known as an azeotrope or constant boiling mixture). It goes on to explain how this complicates the process of fractionally distilling such a mixture.

This is the final page in a sequence of three pages.

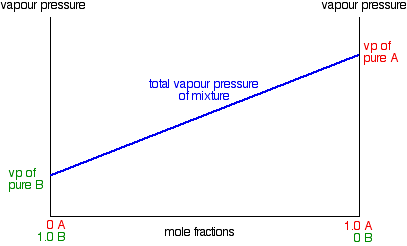
Vapour pressure / composition diagrams for non-ideal mixtures

You will remember that, because of Raoult's Law, if you plot the vapour pressure of an ideal mixture of two liquids against their composition, you get a straight line graph like this:

In this case, pure A has the higher vapour pressure and so is the more volatile component.

It is essential that you are happy with these diagrams whichever way they are drawn. It is really dangerous to get used to always drawing them one way around. You may meet them with all sorts of variations, and so you must understand what is going on.

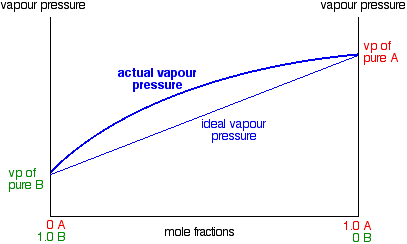
Raoult's Law only works for ideal mixtures. In these, the forces between the particles in the mixture are exactly the same as those in the pure liquids. The tendency for the particles to escape is the same in the mixture and in the pure liquids.

That's not true in non-ideal mixtures.

Positive deviations from Raoult's Law

In mixtures showing a positive deviation from Raoult's Law, the vapour pressure of the mixture is always higher than you would expect from an ideal mixture.

The deviation can be small - in which case, the straight line in the last graph turns into a slight curve.

Notice that the highest vapour pressure anywhere is still the vapour pressure of pure A. Cases like this, where the deviation is small, behave just like ideal mixtures as far as distillation is concerned, and we don't need to say anything more about them.

But some liquid mixtures have very large positive deviations from Raoult's Law, and in these cases, the curve becomes very distorted.

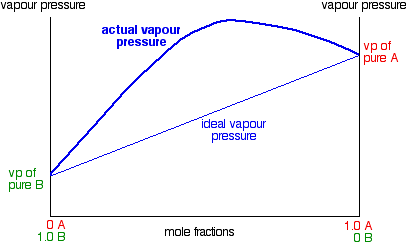
Notice that mixtures over a range of compositions have higher vapour pressures than either pure liquid. The maximum vapour pressure is no longer that of one of the pure liquids. This has important consequences when we look at boiling points and distillation further down the page.

Explaining the deviations

The fact that the vapour pressure is higher than ideal in these mixtures means that molecules are breaking away more easily than they do in the pure liquids.

That is because the intermolecular forces between molecules of A and B are less than they are in the pure liquids.

You can see this when you mix the liquids. Less heat is evolved when the new attractions are set up than was absorbed to break the original ones. Heat will therefore be absorbed when the liquids mix. The enthalpy change of mixing is endothermic.

The classic example of a mixture of this kind is ethanol and water. This produces a highly distorted curve with a maximum vapour pressure for a mixture containing 95.6% of ethanol by mass.

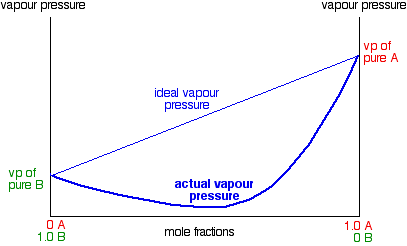
Negative deviations from Raoult's Law

In exactly the same way, you can have mixtures with vapour pressures which are less than would be expected by Raoult's Law. In some cases, the deviations are small, but in others they are much greater giving a minimum value for vapour pressure lower than that of either pure component.

Explaining the deviations

These are cases where the molecules break away from the mixture less easily than they do from the pure liquids. New stronger forces must exist in the mixture than in the original liquids.

You can recognise this happening because heat is evolved when you mix the liquids - more heat is given out when the new stronger bonds are made than was used in breaking the original weaker ones.

Many (although not all) examples of this involve actual reaction between the two liquids. The example of a major negative deviation that we are going to look at is a mixture of nitric acid and water. These two covalent molecules react to give hydroxonium ions and nitrate ions.

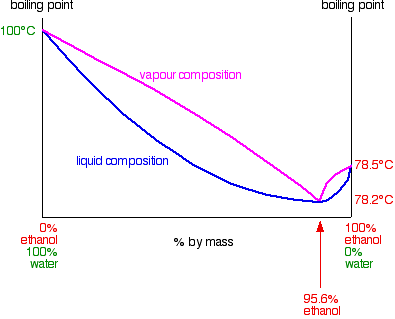
You now have strong ionic attractions involved.

Boiling point / composition diagrams for non-ideal mixtures

A large positive deviation from Raoult's Law: ethanol and water mixtures

If you look back up the page, you will remember that a large positive deviation from Raoult's Law produces a vapour pressure curve with a maximum value at some composition other than pure A or B.

If a mixture has a high vapour pressure it means that it will have a low boiling point. The molecules are escaping easily and you won't have to heat the mixture much to overcome the intermolecular attractions completely.

The implication of this is that the boiling point / composition curve will have a minimum value lower than the boiling points of either A or B.

In the case of mixtures of ethanol and water, this minimum occurs with 95.6% by mass of ethanol in the mixture. The boiling point of this mixture is 78.2°C, compared with the boiling point of pure ethanol at 78.5°C, and water at 100°C.

You might think that this 0.3°C doesn't matter much, but it has huge implications for the separation of ethanol / water mixtures.

The next diagram shows the boiling point / composition curve for ethanol / water mixtures. I've also included on the same diagram a vapour composition curve in exactly the same way as we looked at on the previous pages about phase diagrams for ideal mixtures.

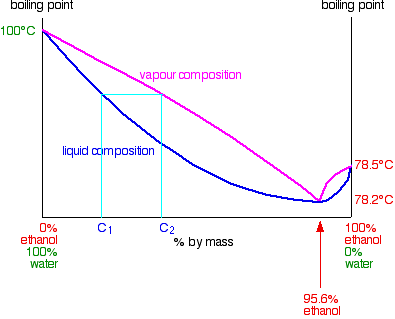
Using the diagram

Suppose you are going to distil a mixture of ethanol and water with composition C₁ as shown on the next diagram. It will boil at a temperature given by the liquid curve and produce a vapour with composition C₂.

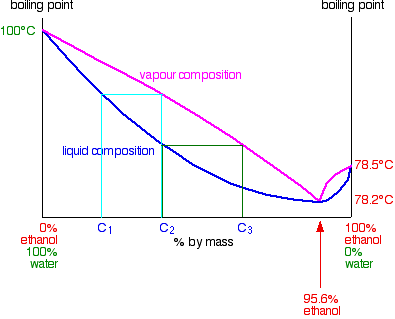
When that vapour condenses it will, of course, still have the composition C₂. If you reboil that, it will produce a new vapour with composition C₃.

You can see that if you carried on with this boiling-condensing-reboiling sequence, you would eventually end up with a vapour with a composition of 95.6% ethanol. If you condense that you obviously get a liquid with 95.6% ethanol.

What happens if you reboil that liquid?

The liquid curve and the vapour curve meet at that point. The vapour produced will have that same composition of 95.6% ethanol. If you condense it again, it will still have that same composition.

You have hit a barrier. It is impossible to get pure ethanol by distiling any mixture of ethanol and water containing less than 95.6% of ethanoll.

This particular mixture of ethanol and water boils as if it were a pure liquid. It has a constant boiling point, and the vapour composition is exactly the same as the liquid.

It is known as a constant boiling mixture or an azeotropic mixture or an azeotrope.

The implications of this for fractional distillation of dilute solutions of ethanol are obvious. The liquid collected by condensing the vapour from the top of the fractionating column can't be pure ethanol. The best you can produce by simple fractional distillation is 95.6% ethanol.

What you can get (although it isn't very useful!) from the mixture is pure water. As ethanol rich vapour is given off from the liquid boiling in the distillation flask, it will eventually lose all the ethanol to leave just water.

To summarise:

Distilling a mixture of ethanol containing less than 95.6% of ethanol by mass lets you collect:

• a distillate containing 95.6% of ethanol in the collecting flask (provided you are careful with the temperature control, and the fractionating column is long enough);

• pure water in the boiling flask.

What if you distil a mixture containing more than 95.6% ethanol?

Work it out for yourself using the phase diagram, and starting with a composition to the right of the azeotropic mixture. You should find that you get:

• a distillate containing 95.6% of ethanol in the collecting flask (provided you are careful with the temperature control, and the fractionating column is long enough);

• pure ethanol in the boiling flask.

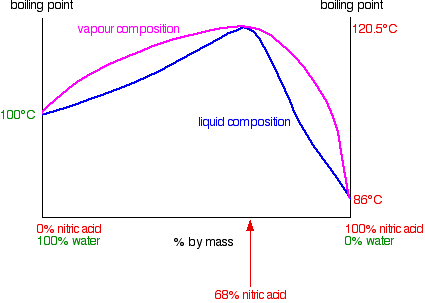
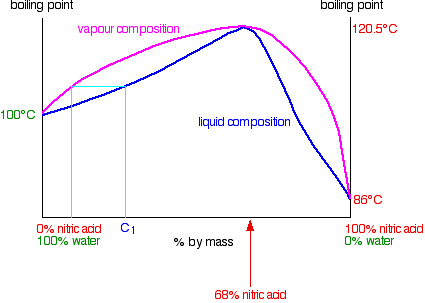
A large negative deviation from Raoult's Law: nitric acid and water mixtures

Nitric acid and water form mixtures in which particles break away to form the vapour with much more difficulty than in either of the pure liquids. You can see this from the vapour pressure / composition curve discussed further up the page.

That means that mixtures of nitric acid and water can have boiling points higher than either of the pure liquids because it needs extra heat to break the stronger attractions in the mixture.

In the case of mixtures of nitric acid and water, there is a maximum boiling point of 120.5°C when the mixture contains 68% by mass of nitric acid. That compares with the boiling point of pure nitric acid at 86°C, and water at 100°C.

Notice the much bigger difference this time due to the presence of the new ionic interactions (see above).

The phase diagram looks like this:

Using the diagram

Distilling dilute nitric acid

Start with a dilute solution of nitric acid with a composition of C₁ and trace through what happens.

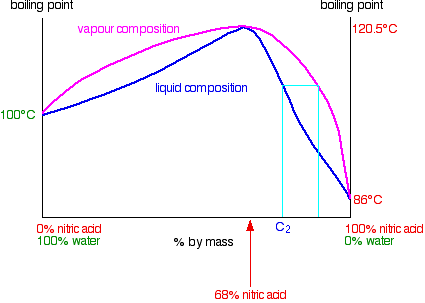
The vapour produced is richer in water than the original acid. If you condense the vapour and reboil it, the new vapour is even richer in water. Fractional distillation of dilute nitric acid will enable you to collect pure water from the top of the fractionating column.

As the acid loses water, it becomes more concentrated. Its concentration gradually increases until it gets to 68% by mass of nitric acid. At that point, the vapour produced has exactly the same concentration as the liquid, because the two curves meet.

You produce a constant boiling mixture (or azeotropic mixture or azeotrope). If you distil dilute nitric acid, that's what you will eventually be left with in the distillation flask. You can't produce pure nitric acid from the dilute acid by distilling it.

Distilling nitric acid more concentrated than 68% by mass

This time you are starting with a concentration C₂ to the right of the azeotropic mixture.

The vapour formed is richer in nitric acid. If you condense and reboil this, you will get a still richer vapour. If you continue to do this all the way up the fractionating column, you can get pure nitric acid out of the top.

As far as the liquid in the distillation flask is concerned, it is gradually losing nitric acid. Its concentration drifts down towards the azeotropic composition. Once it reaches that, there can't be any further change, because it then boils to give a vapour with the same composition as the liquid.

Distilling a nitric acid / water mixture containing more than 68% by mass of nitric acid gives you pure nitric acid from the top of the fractionating column and the azeotropic mixture left in the distillation flask.

Where would you like to go now?

To the phase equilibrium menu . . .

To the Physical Chemistry menu . . .

To Main Menu . . .