|
THE STRENGTHS OF VAN DER WAALS DISPERSION FORCES Towards the bottom of the last page, I described dipole-dipole attractions as being "fairly minor compared with dispersion forces". A student challenged me about this, pointing out that many web sources and books say that dispersion forces are the weakest form of intermolecular attraction. Several sources actually put values on these strengths. Having spent a couple of weeks researching and thinking about this, I still stand by my original statement, and the rest of this page looks at some of the evidence I have found to support it.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Note: If you have come straight to this page from a search engine, it would make sense to read my page about van der Waals forces before you go on. If you are an A level (or equivalent) student, the information on that page is what you will need for exam purposes. This current page is essentially a discussion document to try to get a bit closer to the truth. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Data obtained from calculation There are three main types of van der Waals forces, two of which I have discussed at length on the previous page. These are dipole-dipole interactions (also known as Keesom forces) and dispersion forces (also known as London forces). The third kind of interactions (known as Debye forces) are normally overlooked at this level as being relatively minor compared with the first two. These arise from a permanent dipole on one molecule inducing a temporary dipole in a second one. I need to mention them now, because they crop up in two important sources below. Modern Physical Chemistry by Liptrot, Thompson and Walker, published by Bell and Hyman This textbook was published in 1982 and aimed at A level and introductory degree students. It was only ever accessible to very bright A level students. In the section about van der Waals bonds, they say
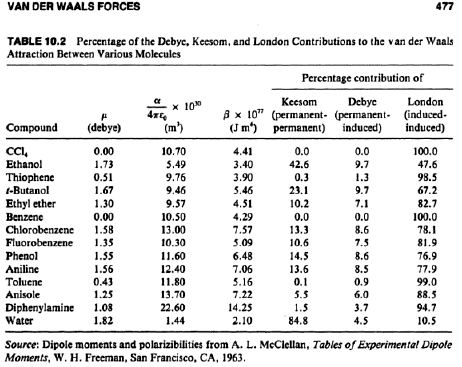
That is then followed by a table showing percentage contributions of the three types of van der Waals forces for a few simple molecules. Three of these are non-polar molecules where the contribution due to the dispersion forces is unsurprisingly 100%. The other two are simple polar molecules, carbon monoxide and hydrogen chloride. Because of the way it is bonded, carbon monoxide has only got a very small permanent dipole.
The hydrogen chloride figures are particularly surprising. HCl has polar molecules, and yet most of the intermolecular forces are due to dispersion forces. Principles of Colloid and Surface Chemistry by Paul C. Hiemenz and Raj Rajagopalan, published by CRC Press, third edition 1997 A Google Books search came up with this table:
The first column of data shows the dipole moments of the various molecules. The second one is a measure of the polarisability of the various molecules. This is a measure of how easy it is for the electrons to move around in the molecule in response to an external electric field - from a neighbouring dipole, for example. (Ignore the third column - it is a term used in the calculation of total intermolecular forces.) Apart from water, and perhaps ethanol, in all the other cases, the London (dispersion) forces make by far the greatest contribution to the overall intermolecular bonding. Notice that the dispersion forces are less important in the molecules which are least polarisable - like water. We'll look at that again in a moment. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Note: If you want to see this table in its original context, this link will take you to the Google Books source. If you are interested in how these figures are derived, you could go back through the previous pages in the book. Unfortunately several pages just before this aren't available from Google. The maths of this defeats me, but I have no reason to suppose that it is wrong. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
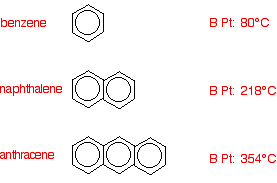
Evidence from boiling points Boiling point is a good guide to the strength of the intermolecular forces. If these are weak, you don't need to supply much energy to break them to produce gaseous molecules, and the boiling point is low. If they are strong, you have to supply a lot of heat energy to break them, and the boiling point is high. Dispersion forces vary enormously from one substance to another Many sources state simply that dispersion forces are weak, and give values for the energy needed to break them. The student who brought this to my attention told me that his teachers were quoting dispersion forces as having a strength of less than 4 kJ/mole. That's typical of the sort of values you can find on the web. This is completely misleading! The size of the dispersion forces is governed by the size and shape of the molecule. You cannot quote a single value as if it was typical of all dispersion forces. If you think about tiny molecules like helium or hydrogen, then the dispersion forces will indeed by very weak. You haven't got many electrons to move around, and very little distance over which to move them. But look at the following sequence of moderately sized molecules. These are all non-polar, and so dispersion forces are the only intermolecular attractions.
If you haven't come across the structure of benzene yet, don't worry about it. Each corner of every hexagon has a carbon atom. The corners with only two lines going away from them also have a hydrogen atom attached. The circles in the centre of the hexagons show delocalised electrons - electrons not firmly attached to a particular atom. Notice that every time you attach another hexagon, the boiling point goes up by about 140°C. By the time you have got to anthracene, the boiling point is quite high. Since this is due only to the dispersion forces between the molecules, those dispersion forces must be strong. I have actually chosen these particular examples because they are non-polar, the delocalised electrons make them very polarisable to give temporary dipoles, and the molecules are flat so that they can lie closely together. The polarisability and the fact that the molecules can lie closely together help to make the dispersion forces strong. But it isn't very difficult to find examples of non-polar molecular compounds with fairly high boiling points, and therefore strong dispersion forces. A more familiar example comes from the fractional distillation of crude oil. Crude oil is a mixture of hydrocarbons of all sizes and shapes. These are non-polar molecules which would be held in the liquid by dispersion forces, and they range from gases to liquids with boiling points over 400°C. There will be a wide range of strengths of the dispersion forces, from the relatively weak in gases like methane to the relatively strong in the sort of hydrocarbons which end up in products like bitumen. Having shown that dispersion forces aren't necessarily weak (in fact, can be quite strong), let's now look at the relative importance of dipole-dipole interactions and dispersion forces. Comparing fluoromethane with ethane This is the example I took on the main page about van der Waals forces. The boiling points of ethane, CH3CH3, and fluoromethane, CH3F, are Both molecules have identical numbers of electrons, and the size of the two molecules is much the same. That means that you might expect the dispersion forces in both molecules to be similar (but see below). Fluorine is the most electronegative element, and therefore the carbon-fluorine bond is going to be very polar. However, even given the large permanent polarity of the molecule, the boiling point has only been increased by 10.2 K. Look at it like this. If there were no intermolecular forces at all between molecules, everything would boil at a temperature fractionally above zero K. (Not actually at zero K - there has to be a little bit of energy to enable movement.) In ethane, the dispersion forces are strong enough that the boiling point has been increased to 184.5 K. Now add the effect of the permanent dipole-dipole interactions to that. The only extra difference the dipole-dipole attraction has made is to increase the boiling point by a further 10.2 K. That is a negligible effect compared with the effect of the dispersion forces. You cannot say that dipole-dipole interactions are stronger than dispersion forces. Part of the problem with this example is that fluorine is so electronegative that electrons in the carbon-fluorine bond are pulled very firmly towards the fluorine atom. That makes the molecule much less polarisable, and so reduces the size of the dispersion forces which depend on temporary movement of electrons in the molecules. So there are two effects operating in opposite directions. The polarity of the carbon-fluorine bond is adding dipole-dipole attractions, while at the same time, the more tightly held electrons are reducing the effect of the dispersion forces. The two boiling points are almost the same. That means that the gain in dipole-dipole attractions is roughly cancelled out by the loss of dispersion forces. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Up-date August 2014: As well as my rough-and-ready way of thinking about it, I am grateful to Thijs van Westen, a PhD student from the Netherlands, for running the fluoromethane case through a modern mathematical model which indeed shows that dispersion forces are the main contributor to the intermolecular bonding in fluoromethane. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
To find out how much effect the addition of the fluorine had on the dispersion forces, I looked at what happened if you lengthened the chain to which the fluorine is attached. In organic chemistry, the effect of putting a very electronegative element in a chain falls off quite quickly along the chain. If the fluorine was having a major effect on the dispersion forces, then there should be a falling-off of that effect as the chain length grows. Is there? Repeating the comparison with longer chains The table shows what happens if you increase the lengths of the chains. Members of each horizontal pair have the same number of electrons and similar length. The higher boiling point for each pair is shown in red.
There are two things you need to notice. First, for all the pairs, there isn't much difference between the boiling points of the members of the pair. In the longer chains, the boiling points, and so the intermolecular forces, of the two members of the pair are still much the same. The effectiveness of the fluorine in disrupting the polarisability of the rest of the molecule will fall as the molecule gets bigger. Since the intermolecular attractions must be much the same for the members of each pair, that implies that the fluorine can't actually be having much effect even in the smaller molecules. Secondly, notice that for the bigger molecules, the alkanes (which don't have a permanent dipole and only have dispersion forces available to them) have slightly higher boiling points than the polar molecules. I can't explain that, but it makes a complete nonsense of saying that a polar molecule will automatically have a higher boiling point than a non-polar one of similar size. Comparing chloroalkanes with alkanes The next table repeats this exercise with chlorine instead of fluorine. Chlorine is bigger and less electronegative than fluorine, and won't have anything like as much effect on the polarisability of the molecules as fluorine does. In order to keep the number of electrons the same, the chloro-compound has to be compared with the alkane with two more carbon atoms. Unfortunately, that makes the alkane slightly longer than the chloride, so the comparison isn't quite as fair as the one with fluorine.
Notice that, again, there isn't all that much difference in boiling points between the members of each horizontal pair. The polar molecule has a slightly higher boiling point than the non-polar one, but not by very much. The increase in intermolecular attractions due to the additional dipole-dipole interactions is almost negligible compared with the effect of the dispersion forces. Molecules with a permanent dipole do usually have a higher boiling point than similarly sized non-polar molecules, but that is because they have dipole-dipole forces as well as dispersion forces. As we have seen, the extra dipole-dipole interactions don't actually add all that much to the boiling point. In conclusion This is just a selection of molecules that I have looked at, but I have decided it is too boring to keep on making the same point over and over. If you are interested, you can easily do this yourself - just try to keep the molecules you are comparing as similar as possible in terms of their shape and length and the number of electrons they contain. Two other series that are worth a look are alcohols, and carbonyl compounds (containing carbon - oxygen double bonds), particularly aldehydes so that the carbonyl group is on the end of a chain. If you believe that hydrogen bonding (in alcohols) is a particularly strong form of intermolecular bonding, doing this for alcohols will upset you! Just as a taster, in the table from the book further up this page, t-butanol is mentioned as having a contribution from dispersion forces of 67.2%. The modern name for t-butanol is 2-methylpropan-2-ol. If you remove the -OH group and replace it with a methyl group you get 2,2-dimethylpropane. Both of these molecules have the same shape and number of electrons. The alkane boils at 282.6 K; the alcohol at 355.4 K. Dispersion forces can be thought of as contributing 282.6° to the boiling point; all the other dipole forces, including hydrogen bonding, an additional 72.8°. Which is the major force holding these alcohol molecules in the liquid? It is the dispersion forces! Finally, then . . .
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Note: My thanks to Professor Alan Campion of the University of Texas at Austin for pointing out a book which deals with this mathematically, and essentially supports my more intuitive conclusions. The book is Physical Chemistry by McQuarrie and Simon, and you would need to look at Section 16-6 with the catchy title "London Dispersion Forces Are Often the Largest Contribution to the r-6 Term in the Lennard-Jones Potential". | |||||||||||||||||||||||||||||||||||||||||||||||||||||
© Jim Clark 2009 (last modified February 2018) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||